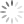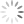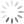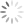(Note from the blog owner: The following is the account by Dr. Lee Wang Yen, a colleague from the Philosophy Department, concerning how he created a computer programme for assessing logic. Since 2016, Dr. Lee has been teaching GET1028 Logic and GET1026 Effective Reasoning for the Department of Philosophy. As both modules are relatively large (200-300 students each semester), we are always looking for ways to streamline or automate processes. This is not just about saving human work; more importantly, it is also about cutting down on human errors and ensuring that our teaching is scalable across larger groups of students without compromising on quality. Knowing a little about what he went through to make his logic assessment program happen, I encouraged him to do a write up for sharing and offered him a platform for hosting it. You can find out more about Dr Lee’s research at http://nus.academia.edu/WangYenLee and contact him at wangyen.lee@nus.edu.sg)
* * * * *
1. Problem
When I first taught GET1028 Logic at NUS, I set a mixture of Multiple Choice Questions (MCQs) and short-answer questions (SAQs). My detailed marking method (deducting 0.1, 0.2, 0.25, etc. marks depending on the seriousness of the mistakes) entailed a huge workload not only for myself, but also for the admin staff in my department, who had to help check the marks calculation. Given the size of my class and the small admin team in my department, everyone was under huge pressure to meet the deadline without compromising on accuracy. I had to work 10-11 hours a day for more than a week. The admin staff had to work over weekends. It occurred to me, given the prompting of the admin staff and department leadership, that I had to change my assessment method.
One option would be to set only MCQs. However, after many long and detailed discussions with Prof. Loy, my deputy head of department (a keen user of MCQs in the large exposure module) in 2017, we came to the conclusion that not all logic skills could be tested by MCQs. While MCQs can test a student’s ability to evaluate a proof, it cannot test a student’s ability to conduct the proof from beginning to the end. As a result, I took up my then teaching assistant’s suggestion and began to write a computer programme that eventually evolved into LogiProof.
2. Development of the Software
I actually first thought of writing a computer programme to grade answers to proof questions in logic assessment in a conversation with my former head of department at another university in 2014. I told him that I had spent much time marking students’ answers to proof questions. It’s time consuming because there is more than one way to prove that an argument is valid (or invalid). Everyone starts with the same premise set and conclusion but is likely to derive further lines in different order. Some even derive different lines. Given that the correctness of each new line a student derives depends on the previous lines he/she has derived, using model answers will be a very inefficient way to grade this kind of question.
If one grades by using model answers, then, for each new question, one has to list a large number of correct proofs that are given to human graders or fed into a computer grading programme. (Some people mistakenly think that my software uses this approach – it doesn’t.) This is too time consuming. The most efficient grading method that can be implemented in a computer programme will use an algorithm that can correctly identify all correct ways of proving an argument (subject to practical limitations) for a large number of proof questions.
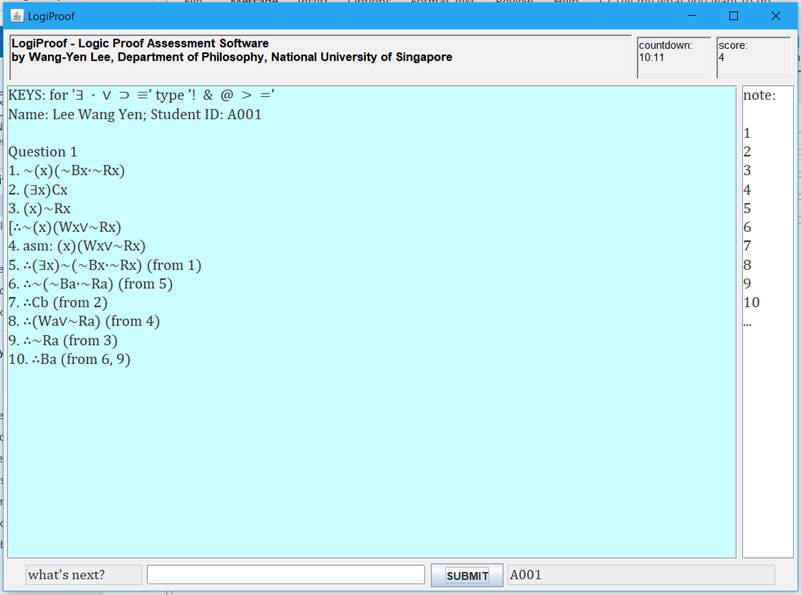
In April 2017 I learnt a new programming language Java to implement such an algorithm. The first version of the software I developed was a command-line interface (CLI) version, as shown here (Figure 1). I took around 3 weeks to write the programme but spent a few more weeks to check the code for errors and make corrections.
Although each student starts at a different time, all students have around 10 minutes to complete the test. The software is programmed to enter blank answers, exit automatically, and generate a result file after 10 minutes and 30 seconds. The software uses three different timers, two of which do not depend on system time. Thus, changing system time won’t thwart them. Attempts to cheat by changing the system time to give a false impression of completing the test within the time limit will result in detectable discrepancies between the system-time-dependent timer and the two system-time-independent timers. In any case, students won’t be able to change the system time of any lab pc as they don’t have administrative privileges.
Upon completion of the test, a result file named after the student’s matric card number will be generated and saved to the desktop. The file contains crucial data such as student’s ID, scores, IP address, start time, end time, elapsed time, and all the answers entered during the test. (The last feature was added after the first run of the test in 2018.) The content of the result file is encrypted using a secret long encryption key that is extremely hard to crack within the few hours a student is given to submit the file. Below is an example of an encrypted result:
‘ht9a50r4aHVecJ2m36YDssiwT2gG/RBN1YOI44SpKgvg
oJKJrDn7m+oGuchyCcwR4WkTvqoYc6p5bWrM/WwXi+
ZkKE1f4tTmJKksUD57e5XPhxRDPJGoLRCSrCffn26kfYyT
T3StKaC35GaiDY7CoPU8LMho/snLHFBvh+kWg3r1PCzI
aP7JyxxQb4fpFoN6KOboXRCNPSaQVN9yZl5yig==’
Students have been told not to tamper with the content of the result file, as any change will lead to failed decryption, which indicates that the file has been modified. Students cannot fake an encrypted result without knowing my secret long encryption key, which I change each time I give a test.
3. New Versions
After I used the CLI version in an actual test in April 2018, some students expressed a preference for a graphic user interface (GUI) version. So I created a GUI version in May 2018 (Figures 2 and 3).
However, the GUI version is a desktop app. Deploying this in a real test requires invigilators to unlock the password protected software using a USB drive for each student. While it won’t take too long, it is still not very convenient.
In June 2018 I learnt two programming languages for web development (Javascript [different from Java] and PHP) to convert the desktop GUI app into a web app (Figure 4). Apart from the ease of deployment mentioned above, the web app has some other advantages over the desktop app.
1. Whereas the desktop app requires a certain version of Java Runtime Environment, the web app can be accessed on any web browser without any additional software, Students can thus take the test on their own laptops, tablets, or even smart phones.
2. The test result is sent to the server directly. There is thus no need to encrypt the result, generate a result file, and ask for submission.
The main advantage of the desktop app over the web app is security. I have now figured out a way to deploy the desktop app without copying it to the local drive of the pc that runs the app. As long as attendance is taken in the pc lab where the test is conducted, it is virtually impossible for a student to arrange for an impostor to take the test without being caught. While the web app requires students to log in using their NUSNET accounts and only provides one access, a student might pretend to take the test in a pc lab or lecture theatre while asking his/her friend to take the test on his/her behalf elsewhere.
The GUI and web app versions allow me to incorporate new features requested by students after the first run in 2018. Below are some of the key changes from the CLI version used in 2018.
1. Both the GUI and web versions display a countdown stopwatch that starts after a candidate sees the first question. In 2018 a student who didn’t manage to finish his test by the time limit took the trouble to write to my head of department and dean to complain that the software didn’t display a timer to indicate the remaining time.
2. Both the GUI and web versions display logical statements using textbook symbols rather than surrogate ones. The original CLI version can’t do this because of encoding limitation. While candidates still have to type logical statements using only surrogate symbols that can be found on a typical keyboard, the input will be automatically translated into one that uses textbook symbols.
3. The GUI version provides real-time translation of a candidate’s input in surrogate symbols into textbook symbols in a textfield next to the input field.
4. Both the GUI and web versions use larger fonts.
5. In response to a request to make the test software more similar to the practice software (LogiCola), I’ve chosen a colour scheme in the GUI version that mimics that of LogiCola.
6. For the deployment of the GUI version in a test, I’ve created a batch file that allows an invigilator to use a USB drive to automatically copy the test software to a workstation, run it, and key in the password. An invigilator arrives 30 minutes before the first round, logs into all pcs using a visitor’s account, and deploys the software using the USB drive. Once all pcs are logged in, it only takes around 4 minutes to deploy the software to all 25 pcs. Students can take the test immediately upon arrival at the lab instead of trying to log in and wait for invigilator to deploy the software. I’ve actually created another batch file that uses a free Microsoft tool that can do the job of this USB drive remotely from the instructor’s pc to all other pcs in a lab. Unfortunately, I was told that the IT centre had disabled some network ports at FASS labs, which blocked this method of deployment.
(Point 6 has become obsolete as I have figured out a way to deploy the desktop app without copying the app to the local drive.)
4. Use of the Software in Student Assessment
The teething problems I encountered in the first run of the computerised test in April 2018 were mainly down to the use of a large but poorly maintained lab outside FASS. However, I was glad that there were no software related issues. The recently concluded computerised test in April 2019 was moved to four very well-maintained pc labs at FASS. As a result, there were no lab related issues at all. Unfortunately, about 10% of the students were affected by a specific bug in the software. All students affected by this bug got into an infinite loop where the app kept displaying the same line after a certain sequence of lines were entered.
Upon checking my code after the test, I identified the bug within a few minutes – I carelessly left out this part ‘replace(“%”, “”)’ in my code. After appending it to the right places the bug was removed. This was entirely my fault and I apologised to my students unreservedly. All affected students were given a replacement test with different questions a few days later. The replacement test was conducted successfully without any errors.
Whilst it was a very straightforward bug that should have been detected earlier, that it was not detected earlier does not mean that I didn’t do a thorough check on my code. When I developed the original CLI version in 2017, I did a thorough check by running it on all the proof questions in the relevant chapters of the main textbook. For each question I tried to key in all wrong answers and a few sets of all correct answers. Although it was a very tedious and rather painful process, it was helpful in revealing bugs, which allowed me to address them. When I subsequently developed the GUI and web versions, I didn’t have enough time to run them on all proof questions in the relevant chapters, though I ran them on many questions. Initially I thought that the missing ‘replace(“%”, “”)’ was left out when I manually converted the original CLI version into the current GUI version. However, I subsequently checked the code of the CLI version and found that the ‘replace(“%”, “”)’ was missing there as well.
Why was this bug not revealed in my thorough testing of the CLI version in 2017? First, the testing process is not fool-proof. If all arguments in the relevant textbook chapters work correctly on the software, it makes it very probable that it will work correctly on other arguments of similar complexities. However, improbable events do happen. Second, I have an explanation for why an improbable event happened in this case. Although this particular bug is very easy to detect when one runs a diagnostic test (by displaying just one of the many silent processes) after becoming aware of a problem it caused, it does not cause problems often enough to be detected in testing. It is partly related to my testing procedure. I tested the app by keying in all wrong answers and a few combinations of all correct answers. However, this bug only causes a problem in a combination (or perhaps a few combinations) of both correct and wrong answers. Specifically, there must be a Q before (Q@~K) and the user must have made a mistake in the subsequent line after keying in (Q@~K) for the infinite loop to happen. If one keys in a correct line after (Q@~K), the bug will not cause any problem. That explains why only around 10% of 302 test takers were affected. Anyway, I’m glad that the bug has been detected and removed.
I’m quite confident that software related errors caused by unidentified bugs are much less likely to occur in future iterations of the computerised test. This is because I have now stopped developing new features for both the GUI and web versions of the app. This allows me to run these two sets of stable code through all the arguments in the relevant textbook chapters all over again and more thoroughly.
5. Discussion on Student Feedback
Over the years I’ve obtained some feedback on the computerised test. As in most issues, there are both positive and negative comments. Most of the negative comments I received after the first run in 2018 had to with the poorly maintained lab outside FASS we used. Since we moved to pc labs at FASS, we have not had any lab-related issues.
One of the most useful suggestions I received in 2018 was that tutorials should be held in a pc lab so that students would have an opportunity to practise using the software. In 2019 all logic tutorials were held in a pc lab. In each tutorial, around 5 minutes were devoted to demonstrating the use of LogiProof. Students were also given 5 minutes to explore the software on their own.
A more important type of comment concerns the grading policy coded into the programme. In both 2018 and 2019, students expressed their concern about the software’s harsh grading policy in that any mistakes, including typos, were penalised with the same severity. While it is admittedly harsh, a quick glance at the 2019 results indicates that that there aren’t a lot of typos. The greatest factor of losing marks is the failure to complete the second question when the time was up (shown by the blank answers towards the end of the second question). The stringent grading of the software has instilled the discipline of typing well-formed formulas. However, at some point I conceded that the policy was indeed too harsh, and subsequently modified my desktop app to implement a more lenient policy. The new version of the app, to be deployed in 2020, will recognise three types of typos (errors related to brackets, wrong cases, additional spaces between characters) and reduce their penalty by 50%.
Some students think that the computerised test is unnecessary, since MCQs suffice to test students’ logical skills and understanding. However, as mentioned above, after careful deliberation and discussion, we concluded that MCQs were not sufficient.
Like mathematical skills, logical skills are multi-dimensional. One who is good at mental arithmetic may not be very good at applying mathematical concepts or theorems to unfamiliar situations that are quite different from the examples used in a textbook. One who is very efficient in getting the correct numerical answers might not be very good at doing a rigorous mathematical proof in number theory. Likewise, there are various aspects to logical skills. One who has a very solid conceptual grasp of logical rules and principles, who understands the concept behind the method of proof by contradiction, the reason behind the inferential rules used in proofs, the point of dropping quantifiers, the relationship between the refutation box and a possible world and the truth conditions of quantified statements, etc., might not be as fluent at applying various rules and methods in solving logical problems (perhaps because he spends more time trying to understand the reason behinds the rules than to practise using these rules). On the other hand, one who is very fluent at applying rules might score A+ in logic exams that mainly test one’s ability to apply various rules and methods, whilst having a poor understanding of logical concepts and the rationale behind logical rules and methods. Both skills are valuable and can be useful in different circumstances.
The different assessment components in this module are designed to test these different kinds of logical skills. In IVLE quizzes, where students are given 48 hours to think, read around, and discuss, the skills tested are quite different from those tested by class quizzes and the computerised test, which involve much shorter time limits. In the latter, fluency at rule application and so-called ‘logic computational speed’ play a crucial role. It’s good to be reflective about logical concepts, rules and methods. Hence the IVLE quizzes. It’s also good to be able to make logical inferences quickly and accurately under the pressure of time. Hence the class quizzes and the computerised test. The final exam has some elements of both kinds of test.
We should not dismiss the logical ability of one who is very fluent at applying rules but has a poorer grasp of logical concepts and the rationale of logical rules and methods, or one who has a very good grasp of logical concepts but is not very fluent at applying logical rules, or one who has the rules at his fingertips but just can’t perform to his true ability when put under the stress of a testing condition with a strict time limit. That’s why we have those various components mentioned above. However, whilst it’s good to be good at one or two aspects of logical skills, it’s obviously better to be good at most aspects. Given the highly competitive nature of this module, it’s not unreasonable to filter the top who excel in all aspects from the good who excel in a few aspects, especially when we are required by the university to do this. The role of the computerised test should be seen in this broader context.
I have also received feedback that expresses ‘strong belief’ that the computerised test software shouldn’t penalise students for using stand-alone small letters for atomic propositions. I beg to differ. Testing knowledge of and skills in the formal method of proof taught in the textbook includes testing knowledge of propositional and quantificational languages, which incorporates all the rules for forming well-formed formulas (i.e. the syntaxes). If a history lecturer penalises an answer to an essay question for a grammatical mistake, one might argue that it is too harsh, as English grammar is not the focus of that assessment. However, the same cannot be said of a grammatical error in an English language test. A student’s command of propositional and quantificational languages is one of the many focusses of the computerised test, some quizzes, and the final exam. Using a stand-alone small letter violates the fundamental rules of both propositional and quantificational languages. A small letter refers to a particular entity which constitutes the subject of a complete atomic proposition. It can never be used alone for an atomic proposition.
Some students pointed out that LogiCola, a different software that I encouraged students to use in preparation for the computerised test, quizzes and final exam, accepted small letters when capital letters ought to be used. The claim is inaccurate. What happens is that if you use small letters by mistake, the software automatically changes the small letters into capital letters. Thus, LogiCola does not accept small letter inputs. It autocorrects the wrong inputs without penalising the student. However, LogiCola is a training tool, whilst LogiProof is an assessment tool. It’s not reasonable to expect an assessment tool to adopt the same lenient policy used in a training tool.
There is view that a problem with the computerised test is the need to learn an additional notation (notation is a set or system of symbols), which a student claimed to be ‘extremely disorientating’. I don’t think this is a good objection.
Using two or more corresponding notations is not uncommon in other disciplines or subjects. In music we have Nashville number system (1 -do; 2 – re; 3 – mi etc.) and the system used in musical scores. Music students who struggle with converting one notation to another in real time shouldn’t blame the music teacher or inventors of these notations. They should just concede that they are not good enough, as there are music students and teachers who can do this very fluently. In probability, the axioms of probability calculus are expressed in logic notation and its corresponding set-theoretic notation. In discrete mathematics you’ll learn Boolean algebra, a notation from which the corresponding logic and set-theoretic notations are derived. So you have to basically juggle with three corresponding notations (e.g. ‘+’ [Boolean] corresponds to ‘∨’ [logic] corresponds to ‘∪’ [set-theoretic]). In calculus you have Lagrange’s notation and Leibniz’s notation.
Even if one is not interested in all the other subjects mentioned above, and is only interested in logic and its cognate subjects, one will still encounter different logic notations sooner or later. Different books and journals use different logic symbols. If you read a book in philosophy of science, e.g. Howson & Urbach Scientific Reasoning, you’ll find a logic notation that is different from that used in the main textbook adopted in this module. If you study logic (or try to reinforce your knowledge of logic) in discrete mathematics, e.g. in Susanna Epp’s textbook, you’ll use p∧q (Yes, small letters for atomic propositions! Yes, without brackets!) for conjunction, p→q for conditionals, and p for bi-conditionals.
Students should see the need to juggle with two notations in this module as an opportunity to hone an essential skill that they will need anyway to further develop their knowledge of and skills in logic and its cognate subjects. Given the small number and extreme simplicity of the symbols (compared with those used in maths and physics) we learn in each of these two notations (~, &, @, >, =, (!x), (x)), and the close correspondence to the keys used in LogiCola (except for = and @), I fail to see any justification for this complaint.
A student commented that reading the computerised test symbols was like reading Chinese. This seems to be a metaphorical way of saying that these symbols are very difficult. Even if Chinese is really that difficult, bilingualism or multilingualism is a good thing. Some research suggests the cognitive benefits of being bilinguals. For example, ‘Researchers have shown that the bilingual brain can have better attention and task-switching capacities than the monolingual brain, thanks to its developed ability to inhibit one language while using another. In addition, bilingualism has positive effects at both ends of the age spectrum: Bilingual children as young as seven months can better adjust to environmental changes, while bilingual seniors can experience less cognitive decline.’ (https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3583091/). I thank my government and parents for ‘insisting’ that I learn three languages (although the former wanted me to learn two, and the latter wanted me to learn two, and there is one in the intersection). I hope students can see the value of learning more than one logic notation.
6. Reflection
Some may think that going through all these troubles to develop LogiProof is an overkill or perhaps too demanding. Given the practical problems we faced in 2017, I didn’t really have much of a choice. How do I feel about the need to develop this software to solve a practical teaching problem? I have mixed feelings, though most of them are positive.
First, I thoroughly enjoyed the process of learning new programming languages and coding the software. In a sense, the practical problem has given me a good ‘excuse’ to indulge in what I love. While I have no formal training in programming (the closest thing to a formal training was some BASIC and PASCAL programming that I learnt in an after school computer class I took in my primary school years, though I wasn’t really interested in it at that time, as I was mainly interested in taking advantage of the computer class to play computer games – silly computer games such as Pac-Man, Ninja etc), I’ve been an amateur programming enthusiast for some time.
Second, the process of diagnosing bugs and removing them is extremely satisfying. While some bugs were quite difficult to diagnose, I like the feeling that so far I have not failed to diagnose any bugs that had caused the problems that I became aware of in the process of developing and using the software.
Third, I’ve been telling my logic students that logic is useful and practical. Some are rather sceptical about my claim, since a huge chunk of the material is highly abstract. When I started to write the predecessor of LogiProof in 2017, I thought that this was one of the best ways to show my students that logic was very useful and practical. Logic enabled me to learn these programming languages quickly to implement an algorithm to do and evaluate logical proofs automatically, which helped me to help students learn logic. (While there is some element of circularity here, we shouldn’t worry about this since I don’t intend to justify basic logical principles using LogiProof. In fact, LogiProof assumes that basic logical principles are truth-conducive without trying to prove them. While logic can be taught by non-philosophers, we need philosophy when it comes to the justification of basic logical principles. This is the province of epistemology.) Some of my scientist friends in Cambridge commented that philosophers were erudite but impractical people. I hope the development of LogiProof can help in a small way to address that concern.
The only negative feeling I have about this process is that it has used up so much of my time that I badly want to spend on my research projects in philosophy of science. Despite my love for teaching and programming, philosophy of science and other core areas in analytic philosophy revolving around my research agenda are still my first love. My soul will not find rest until I can get back to grappling with these issues.
In sharing all these, I’m not suggesting that instructors in a similar situation ought to do something similar, e.g. everyone teaching a big class should write a computer programme to help with assessment and grading. As explained at the beginning, computers are the most efficient graders of logic proofs given the nature of such proofs. Although I lack formal training in computer programming, the subject to which I need to apply computer programming happens to be the conceptual foundation of computer programming, which makes it easier for me to pick it up without formal training. These two conditions that make the computerisation of logic proof assessment appropriate may not hold in other modules.
In some modules perhaps MCQs suffice, and there is no need to further automate the grading of MCQs as there is already a sufficient degree of automation even when bubble forms are used. In some subjects, human graders are still needed to do the job properly. For example, I have been told that despite the progress in artificial intelligence, adequate natural language translation still requires human translators. See how Google Translate fumbled with the Chinese and Malay translations of this English sentence ‘Everything that is both cat and dog (hybrid species) is animal’. The Malay translation is closer, but still wrong.
Perhaps the following general principle that can be extracted from my experience with developing LogiProof is useful to instructors of other subjects. If you face a practical problem in teaching a subject, you might want to explore how you can make use of your existing skills to acquire some related skills to develop a tool that addresses the problem. The tool can be purely conceptual and may not always involve the use of technology. I was told that a colleague in biomedical chemistry who specialised in the more computational part of biomedical sciences made use of his considerable skills in computation to develop text analytics that he applied to analyse qualitative student feedback on teaching. This seems to be an instance of this general principle.