C.-H. Wang & Z. Tong “On the Density Waves Developed in Gravity Channel flows of Granular Materials”, J. Fluid Mech., 435, 217-246 (2001).
C.H. Wang and Z. Tong, “Transient Development of Instabilities in Bounded She ar Flow of Granular Materials”, Chem. Eng. Sci., 53(22), 3803-3819 (1998).
ABSTRACT
A study has been conducted on the analysis and fate of instabilities arising from rapid shear flow of a granular material. Specifically, this study is made through a detailed analysis of continuum rheological models, to examine whether the initiation and growth of the instabilities predicted by this analysis are consistent with the linear stability theory. It is found that rapidly sheared particles tend to form alternating bands or clusters of high and low solid concentrations. Two types of standing-wave instabilities, namely layering and stationary modes, are investigated. The fate of these density waves is tracked through transient integration of the macroscopic balance equations, and examined by a fast Fourier transform (FFT) analysis. In such a formulation, a few characteristic modes with different wavenumbers have been identified. The temporal evolution of the intensity of fluctuating energy is investigated by analyzing the most dominant mode in the system. It is found that the structure and dynamics of the resulting waves can be quantitatively correlated with the power spectrum density of concentration fluctuations. The development of the layering mode is governed primarily by linear instability. On the other hand, clusters of particles of the stationary mode may stretch and interact with neighbouring clusters. This new finding indicates that the transient development of a two-dimensional stationary disturbance may ultimately lead to a one-dimensional layered structure. The stationary and layering perturbations eventually evolve to a similar structure and the stationary perturbation leads the system to the layered state more rapidly than the layering mode.
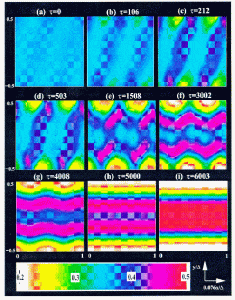
Temporal evolution of the stationary mode in a rapid shear flow of granular materials: Distribution of solid fraction.
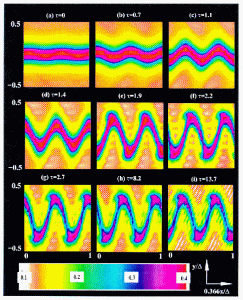
Temporal evolution of the dominant density wave in a gravity-driven channel flow of granular materials: Distribution of solid fraction.
R. S. Deng, C. H. Wang, “Particle Image Velocimetry Study on the Pattern Formation in a Vertically Vibrated Granular Bed”, Physics of Fluids, 15(12), 3718-3729 (2003).
ABSTRACT
In this work, a two-dimensional particle image velocimetry (PIV) system was used to examine the f/2 stripe pattern forming in a vertically vibrated granular layer. Since the PIV sampling frequency does not match with the vibrating frequency, a special identification-coupling method was adopted to combine the images taken in different cycles to offer the information in one complete cycle. The measured velocity vectors showed exactly the particle motions at various statges of a motion cycle, illustrating the alternating peaks and valleys on the layer top. Furthermore, quantitative results on the temporal evolution of velocity profiles were obtained and some other interesting phenomena were observed, such as the appearance of local structures (e.g., dual-phase layer structure) and the moving feature of the “standing point.” The mechanism accounting for the occurrence of stripes on the surface is discussed.

(a)

(b)
The occurrence of lateral particle velocity: (a) a snapshot in the plate-upwards-moving stage. (b) a snapshot in the plate-downwards-moving stage.
R. S. Deng, C. H. Wang, “Instabilities of Granular Material Undergoing Vertical Vibrations: a Uniformly Driven Layer”, J. Fluid Mech. 492, 381-410 (2003).
ABSTRACT
In this work, the stability of a uniformly driven granular layer is examined by linear stability analysis. This includes two main steps: first the base state at various values of mass holdup (Mt) and energy input (Qt) is calculated; and, secondly, small perturbations are introduced to verify the stability of the base state by solving the linearized governing equations and corresponding boundary conditions. Results from the base-state solution show that, for a given pair of Mt and Qt, solid fraction tends to increase at first up the layer height and then decrease after a certain vertical position. In contrast, granular temperature decreases rapidly from the bottom plate to the top surface. The stability diagram is constructed by checking the eigenvalues at different points in the (Mt, Qt) plan, and their dependence on the operating conditions and materials properties is also investigated. For the unstable regime, pattern formation is illustrated with the variation of solid fraction with vertical position. For the layer mode, there are no variations at different horizontal positions. In contrast, a periodic feature is found for the stationary mode in which alternating particle clusters and voids are observed in the horizontal direction. By introducing perturbations in different directions, we have produced surface patterns such as strips, squares and hexagons. Besides the solid fraction distribution, other variables such as the profiles of velocities and granular temperatures are also examined.
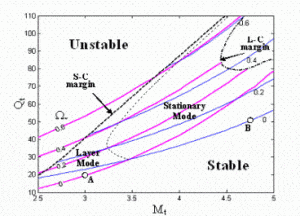
(a)

(b)
(a) Stability diagram showing the contours of Ωr, Ωr =0 is the neutral stability contour. Ωr >0 and Ωr < 0 are the unstable regimes, respectively. The thick and thin solid grey curves are the real parts of the L-C and S-C eigenvalues, respectively. The thin dashed curve is the dividing line between the layer mode and the stationary mode. (b) Contours of Ωr in the (Kx, Kz) –plane, (Mt, Qt)=(3.0, 19.83).